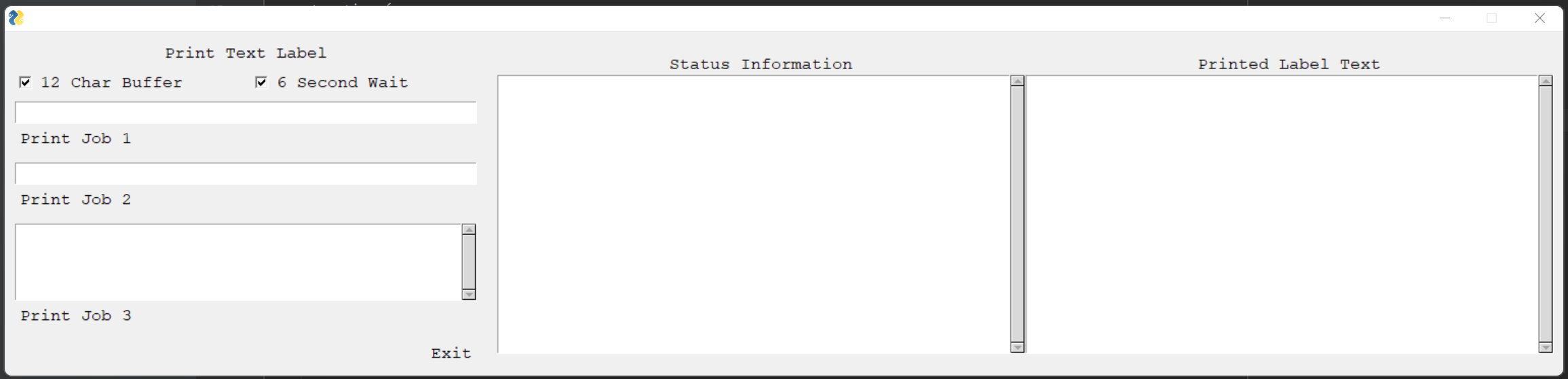
Programing Portfolio
Contact:
scott.sattler.dev@gmail.com
Certifications:
Certified Associate in Python Programming
Certified Entry-Level Python Programmer
CompTIA A+ // TODO:
Coursework:
CS50: Introduction to Computer Science
6.034: Artificial Intelligence
Relative Competency (highest to lowest):
Python, C#, HTML/CSS/JS, SQL, R
GitHub:
https://github.com/scott-sattler
Quick Links:
"""
Given an integer array nums and an integer k, return the k most frequent elements, in any order.
"""
class Solution:
def topKFrequent(self, nums: List[int], k: int) -> List[int]:
# create frequency map
freq_m = dict()
for num in nums:
freq_m[num] = 1 + freq_m.get(num, 0)
# heapify for k O(log2 n) pops
import heapq
freq_list = [(-v, k) for k, v in list(freq_m.items())]
heapq.heapify(freq_list) # O(n) < O(k log2 n)
# pop k times for O(k log2 n) complexity
top_k = list()
for _ in range(k):
top_k.append(heapq.heappop(freq_list))
return [k for v, k in top_k] # return only relevant data
live solutions
https://leetcode.com/scott_sattler/
frontend <-> gateway <-> backend
- pick an image file to upload
- select a pixel on that image
- receive the name of the selected color
// TODO: clean up pre-alpha demo; upload copied project

view source
download pre-alpha (unzip then run .exe)
// TODO: update

view source
download app
My first application! Was fun. Self imposed constraint to solve independently.

view source
download app
// TODO: replace placeholder example
Starting with a 1-indexed array of zeros and a list of operations, for each operation
add a value to each the array element between two given indices, inclusive. Once all
operations have been performed, return the maximum value in the array.
public static long ArrayManipulation(int n, int[][] queries)
{
long[] manipulated_array = new long[n + 1];
long sum = 0;
long maximum_value = -long.MaxValue;
for (int i = 0; i < queries.Length; i++)
{
manipulated_array[queries[i][0] - 1] += queries[i][2];
manipulated_array[queries[i][1]] += -queries[i][2];
}
foreach (long element in manipulated_array)
{
sum += element;
if (sum > maximum_value)
maximum_value = sum;
}
return maximum_value;
}
To improve a calculation where normal (Gaussian) distributions were typically used, I derived the following conditional CCDF (conditional complementary cumulative distribution function):
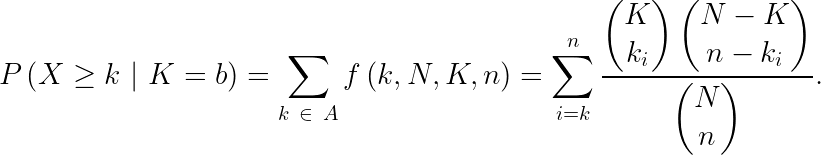
Given the circumstances of the calculation, the following constraints were imposed:
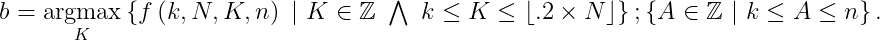
And to improve clarity, R was used to plot the results of the study.
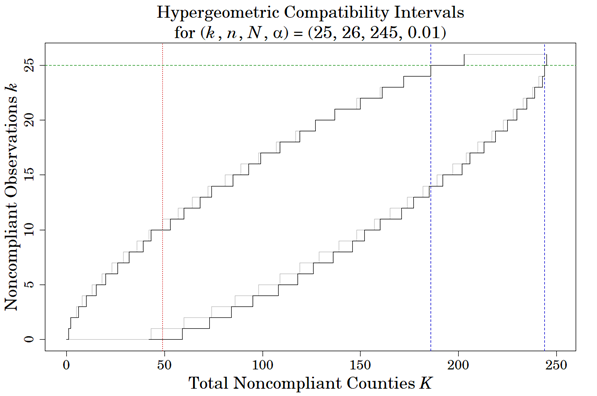
The black step functions were generated from exact admissible two-sided intervals. This calculation used Weizhen Wang's work published in the Journal of the American Statistical Association (2015, vol. 110, p. 1491). The grey underlaid step functions are hypergeometric quantile (inverse CDF) functions of the same parameters.
light/dark mode (copy course doc)?
screen size compatibility
javascript | every link: target="_blank" rel="noopener noreferrer"
css/html | more clean up
new style? https://www.w3schools.com/howto/tryit.asp?filename=tryhow_js_tabs
name consistency
chess README.md first project
upload A* project portfolio copy
finish porting weather app to dash and upload new screens
bit more cleanup
remove and replace old projects
add at least one project that accentuates strengths
and accurately reflects current ability...